I have been solving exercises of Neural Networks and Deep Learning Book by Michael Nielsen. If you are following along my solutions, that’s great. Thank you so much! If not, here is link to Chapter 1 Exercise 1.1 Solution about Sigmoid neurons simulating perceptrons, part I
Following is my attempt to second exercise:
Exercise 1.2
Sigmoid neurons simulating perceptrons, part II
Suppose we have the same setup as the last problem - a network of perceptrons. Suppose also that the overall input to the network of perceptrons has been chosen. We won’t need the actual input value, we just need the input to have been fixed. Suppose the weights and biases are such that \(w \cdot x + b \neq 0\) for the input \(x\) to any particular perceptron in the network. Now replace all the perceptrons in the network by sigmoid neurons, and multiply the weights and biases by a positive constant \(c > 0\). Show that in the limit as \(c \rightarrow \infty\) the behaviour of this network of sigmoid neurons is exactly the same as the network of perceptrons. How can this fail when \(w \cdot x + b = 0\) for one of the perceptrons?
Solution:
We are asked to keep the same setup as in Exercise 1.1. Refering to that,
\[\begin{eqnarray} \mbox{z} = \left\{ \begin{array}{ll} 0 & \mbox{if } w\cdot x + b \leq 0 \\ 1 & \mbox{if } w\cdot x + b > 0 \end{array} \right. \tag{1}\end{eqnarray}\]
we saw for perceptrons, \((w \cdot x + b)\) multiplied by positive constant \(c > 0\) does not affect the result of \(cw \cdot x + cb = 0\) or \(cw \cdot x + cb > 0\). Similarly, squashing function sigmoid doesn’t have any effect on behaviour of network given output \(z\) have values at extremities.
To explain that extremities point further,
As we have seen in the first chapter, Sigmoid function looks like this:
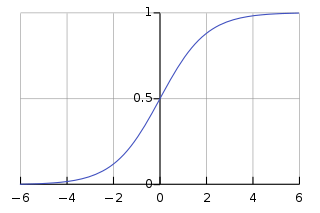
Algebraically, Sigmoid function is represented as:
\[\begin{eqnarray} \sigma(z) \equiv \frac{1}{1+e^{-z}}. \tag{2}\end{eqnarray}\]
When \(z \equiv w \cdot x + b\) is a large positive number. Then \(e^{-z} \approx 0\) and so \(\sigma(z) \approx 1\) (asymptotically). To put it in the words, when \(z = w \cdot x+b\) is large and positive, the output from the sigmoid neuron is approximately \(1\), just as it would have been for a perceptron. By referring to above diagram, we can say \(\sigma(z) > 0.5\). On the other hand that \(z = w \cdot x+b\) is very negative. Then \(e^{-z} \rightarrow \infty\), and \(\sigma(z) \approx 0\) (asymptotically). So when \(z = w \cdot x +b\) is very negative, the behaviour of a sigmoid neuron also closely approximates a perceptron. Again by referring to above diagram, we can say \(\sigma(z) < 0.5\). Here, the determination of 0.5 has not much effect. However, when \(w \cdot x+b = 0\) i.e., \(\sigma(z) = 0.5\) catergory of the result cannot be judged, so the binary classification is difficult to perform and this is where behaviour of sigmoid neurons deviates from the perceptron model.
If above paragraph seems difficult to grasp, always refer to diagram after each sentence, it would help to understand the theory more concretely.
Thanks for reading! Hope you found it helpful. If you have any doubts or found any mistakes please comment below.
Will post rest solutions soon.